AI Models Demystified – Part 1: Linear Regression

Welcome to the first post in my new series where I attempt to peel away the intimidating layers of AI models. This one’s for you – the curious beginner who keeps hearing, “I’m building an AI model,” and wonders what that actually means. If you’re already knee-deep in neural nets and transformers, feel free to stick around for some nostalgia or to chuckle at my analogies – and do drop a comment with your thoughts!

LLMs: The New Kid on the Block

In today’s AI buzz, terms like ChatGPT and Generative AI (GenAI) have become the poster children. Large Language Models (LLMs) are the new celebrities of tech. But AI per se isn’t new. It dates back to 1956, when the term was first coined at the Dartmouth Conference. Back then, the models weren’t exactly charming. They didn’t write poems or argue philosophy with you. They were expert systems and rule-based engines that performed decision-making with structured datasets, often in areas like medical diagnosis and credit approval.

ChatGPT truly brought in the ‘Golden Age of AI’. Much before this golden era, many attempts were made by AI scientists and data scientists to usher it in — but they failed to sustain momentum. In fact, AI suffered its own version of a recession between 1987 and 1993, when enthusiasm and funding dried up. Even when IBM’s Deep Blue beat Kasparov in 1997, the AI hype didn’t catch on with the masses. Why? Because those models didn’t talk back. (Seriously, what’s the fun if your AI can’t sass you?)Then came Transformers in 2017. Not the Michael Bay variety, but a now-legendary paper titled “Attention Is All You Need”, led by Ashish Vaswani. That was the quiet birth of modern LLMs. But more on that in a future post.

Where Should You Start?

If you want to understand AI, don’t start with LLMs. That’s like skipping undergrad and directly applying for a PhD program. Unless you’re a prodigy, it’ll leave your brain spinning faster than a roulette wheel.

Instead, let’s start with something more familiar. Something most of us learned (and quickly forgot) in high school: Linear Regression.And yes, I literally mean high school algebra. That Y = mX + c stuff? That’s your first AI model right there. No kidding.

Back to the Basics: Y = mX + c

Even if you don’t remember the term linear regression, I bet the equation y = mx + c rings a bell. Or maybe you’ve seen it dressed in fancier clothes like Y = Xβ + ε. It’s just the equation of a straight line, where:

• X is the independent variable (the thing you control or observe)
  
• Y is the dependent variable (the thing you’re trying to predict)
  
• m is the slope of the line
  
• c is the Y-intercept
  

Maybe you don’t remember the equation, and that’s perfectly fine. Perhaps you’re more of a visual learner—the kind who remembers graphs and pictures better than formulas and symbols. If that sounds like you, then the graph below might stir up some distant memories from math class.

If you don’t remember the equation or the graph, don’t worry—not even a little. You’re in the right place. I’ll walk you through how this all connects to AI, step by step, without assuming any prior knowledge. So grab a coffee, sit back, and keep reading—you’re about to understand more than you think!

An Example: Yoga Pants and Demand

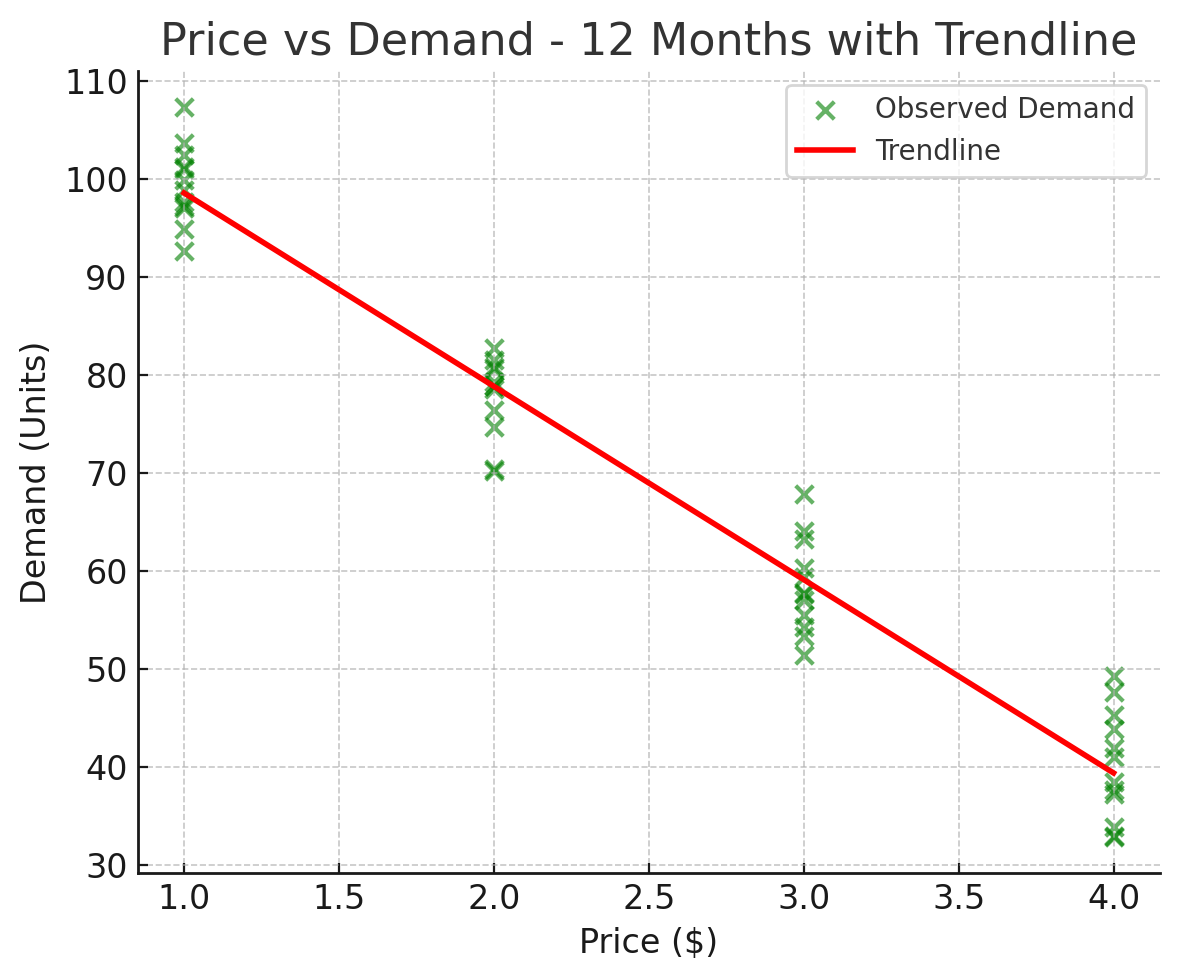
Let’s say you’re selling yoga pants online. You start by pricing them at $1 – they sell like hotcakes. Next week, you bump the price to $2. Fewer buyers now, but still some. Then $3, and even fewer. Eventually at $4, your grandma buys one out of pity.

Plot this on a graph:

• X-axis: Price
  
• Y-axis: Demand (units sold)
  

What you’ll see is a downward trend. More price = less demand. No rocket science.

If you repeat this changing price pattern every month, you get a nice scatter of dots across the chart. 

Now, to find the pattern, you draw a straight line that best fits these dots. It won’t touch every dot, but it should run as close to as many as possible. This, my friend, is regression.

Back in school, you eyeballed it using a ruler. Your high school teacher told you to move around the ruler on the graph till you thought you found the right place to draw the line which is close to most of the dots. When you moved that ruler around, your mind built the first AI model at that time. It was not exactly AI though, it was Natural Intelligence that did it [refer to my previous article if you want to debate natural vs artificial intelligence]. In AI, the algorithm does that job for you – but mathematically.

That Line? That’s Your Model

Now we started with Y = mX + c and we now ended up with a straight line on this graph. What’s the relationship between these two? The equation Y = mX + c is nothing but an algebraic version of the straight line. It’s like translating English (graphian) to French (algebrian)—same message, different language.

[By the way, “algebrian” and “graphian” are not real words in the dictionary, but they should be.]

Now an algebrian will look at this specific graph and translate it into an equation like:

Y = -20X + 120

Let us test this equation:

• At $1: Y = -20(1) + 120 = 100 units
  
• At $2: Y = -20(2) + 120 = 80 units
  
• At $3: Y = -20(3) + 120 = 60 units
  

If I ask you, “When prices go up, what happens to demand?” — both the algebrian and graphian will say demand comes down.

Now, what will the demand be if the price is $2.5?

• The graphian will put his finger on the graph at $2.5, trace up to the trend line, and say “70 units.”
  
• The algebrian will scribble on a paper: Y = -20 × 2.5 + 120 = 70 units.
  

Same answer, two different approaches.You can now predict demand at any price. You’ve just built a predictive AI model using high school algebra. Boom.

But How Does AI Really Fit the Line?

Now, has all the high school math come rushing back into your mind? And what about that close friend who was sitting next to you in that algebra class? Those were the best times, weren’t they!

By now I can hear your mind voice asking me, “All this is fine, but you promised to teach me AI model and here we are learning algebra — which I knew already.”

You’re right. The main point I want to convey is that you already know how the basic AI model works. Remember how in high school you picked up your ruler and moved it around the graph to draw a line touching almost all the dots (but not all)? A linear regression AI model does exactly that, but mathematically.

Here’s how AI fits the line using a complex algorithm. It calculates the distance between the actual Y value and the predicted Y value for each data point and tries to minimize this distance. This method is called least squares.

The error for one data point:
Error = Y_actual – Y_predicted

To avoid canceling out positives and negatives, we square the errors and compute the average:
Loss (MSE) = ∑ (Y_actual – Y_predicted)² / nThis is Mean Squared Error. The model adjusts the slope (m) and intercept (c) until this error is as small as possible for every point on the graph. That’s how it learns from data.

In essence, your AI model is just finding the best version of Y = mX + c that fits your data.

Why Does This Matter?

You might ask, “Why go through all this?” Because once you have the line, you no longer need the entire dataset to make predictions.

• Got a new price? Predict demand.
  
• Got a new marketing spend? Predict sales.
  

Prediction is power. Entrepreneurs use it to guess if their idea will fly. CEOs use it to foresee revenue. Heck, even ChatGPT predicts the next word in a sentence (stay tuned for my future blog on that).

AI is Just Algebra in Disguise

In this case, the AI model is nothing but a formula or the equation Y = mX + c. That’s it, my friend! That’s it! [This is the favorite phrase of my teacher AI professor at UT Austin, Dr. Kumar Muthuraman.]

Using this model, you can predict any value of Y as long as you know X. Is the prediction accurate? Well, it’s around 80% accurate. Why not 100%? Because remember — your line doesn’t touch all the dots. It touches most of them, and for the rest, there will be a small error. But it’s a minor error you can live with.

Let me bring it full circle. If someone asks you, “What’s an AI model?” just say:

“It’s basically a fancy equation. Y = mX + c.”

And you’d be 90% right.Of course, modern models get much more complex, but the foundation is this simple. AI isn’t always magic. Sometimes it’s just math in lipstick.

So, What Comes Next?

Now that I have successfully demystified an AI model for you, are you ready to confidently discuss this at your next dinner party? Not quite. Because we’ve only scratched the surface.

There’s more to learn: Supervised vs. Unsupervised learning, Continuous vs. Categorical variables, Signal vs. Noise. Remember, linear regression is baby step 1. There are many steps ahead in this journey. And by the time we get to things like computer vision or LLMs, the connection to linear regression might seem distant — but it’s still there.

Whenever AI gets too complex, do what I do: I mentally trace it back to this simple linear regression model. It works like a charm.

In Conclusion

AI took off because of three converging forces:

1. Massive data storage
   
2. Massive computing power
   
3. Sophisticated algorithms
   

None of these existed when I was in school. Just like calculators — once banned — are now essential tools, AI will soon be everywhere.

Someday, your grandchild will laugh at the idea of manually drawing a trendline. They’ll ask, “You didn’t use AI for that?”

Until then, keep your ruler handy. Or better yet, keep reading my blog.

The next step in your AI journey is just around the corner.

Subscribe to stay updated.

_{Sources & Referrences: Grammarly.com ; ChatGpt}